


Next: About this document ...
CS3331: Numerical Methods
Homework 2
Due date: March. 25, 1998 (Tuesday)
- 1.
- (10%) Use the method of Gaussian elimination to solve, by hand,
the following matrix equation:
![\begin{displaymath}
\left[
\begin{array}
{cccc}
2 & 4 & -1 & -2\\ 0 & 1 & -1 ...
...[
\begin{array}
{c}
-1\\ -5\\ 6\\ 7
\end{array} \right]
\end{displaymath}](img1.gif)
.
- 2.
- (10%) Find LU decomposition, by hand, of the following matrix:
![\begin{displaymath}
\left[
\begin{array}
{ccc}
-1 & 2 & 0\\ 2 & -1 & 2\\ 0 & 2 & -1\\ \end{array} \right]
\end{displaymath}](img2.gif)
.
- 3.
- (10%) Find the inverse, by hand, of the following matrix:
![\begin{displaymath}
\left[
\begin{array}
{ccccc}
0 & 0 & 0 & 0 & 2\\ 0 & 2 & ...
...2 & 0 & 0 & 0 & 0\\ 0 & 0 & 2 & 0 & 0\\ \end{array} \right]
\end{displaymath}](img3.gif)
.
(Note that this is two times a permutation matrix.)
- 4.
- (20%) A simple projection matrix
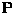 can be expressed as
can be expressed as
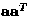 , where
, where 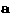 is a unit vector.
is a unit vector.
- (a)
- Prove that a simple projection matrix
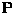 satisfies
satisfies
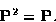
- (b)
- Prove that the trace (sum of diagonal elements)
of a simple projection matrix is always 1.
- 5.
- (20%) A more general definition of a projection matrix
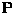 is
a square matrix that satisfies
is
a square matrix that satisfies 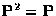 . Use this definition to prove the following two statements:
. Use this definition to prove the following two statements:
- (a)
- If
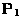 and
and 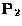 are projection matrices,
then
are projection matrices,
then 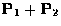 is a projection matrix only if
is a projection matrix only if
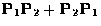 is a zero matrix.
is a zero matrix.
- (b)
- If
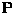 is a projection matrix, then
is a projection matrix, then 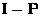 is also a
projection matrix.
is also a
projection matrix.
- 6.
- (30%) Suppose that an invertible matrix
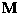 is partitioned
into four submatrices
is partitioned
into four submatrices
![$
{\bf M}=
\left[
\begin{array}
{cc}
{\bf A}& {\bf B}\\ {\bf C}& {\bf D}
\end{array} \right],
$](img15.gif) where
where 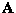 and
and 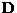 are also invertible.
are also invertible.
- (a)
- Find the inverse of
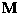 in terms of
the submatrices
in terms of
the submatrices 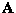 ,
, 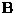 ,
, 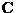 , and
, and 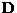 . Specifically, you should start with the identity
. Specifically, you should start with the identity
![$
\left[
\begin{array}
{cc}
{\bf A}& {\bf B}\\ {\bf C}& {\bf D}
\end{array}...
...egin{array}
{cc}
{\bf I}& {\bf 0} \\ {\bf 0} & {\bf I}
\end{array} \right]
$](img20.gif) and expand it into four matrix equations.
Then derive
and expand it into four matrix equations.
Then derive
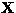 ,
, 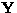 ,
, 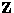 , and
, and 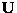 in terms of the
submatrices
in terms of the
submatrices 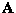 ,
, 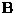 ,
, 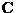 , and
, and 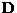 explicitly.
explicitly.
- (b)
- Repeat (a), but start with
![$
\left[
\begin{array}
{cc}
{\bf X}& {\bf Y}\\ {\bf Z}& {\bf U}
\end{array}...
...gin{array}
{cc}
{\bf I}& {\bf 0} \\ {\bf 0} & {\bf I}
\end{array} \right].
$](img25.gif)
- (c)
- Do you obtain the same answer in (a) and (b)?
If yes, prove that the obtained answers are equivalent.
If no, explain why.
Note that:
-
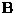 and
and 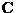 are not necessarily invertible.
So your answers should not include expressions such as
are not necessarily invertible.
So your answers should not include expressions such as
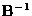 and
and 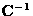 .
. - In deriving the answers, you should be extremely
careful about matrix manipulation techniques.
If you have any questions, feel free to consult
you Linear Algetra textbooks or ask TA.



Next: About this document ...
J.-S. Roger Jang
3/18/1998
![\begin{displaymath}
\left[
\begin{array}
{cccc}
2 & 4 & -1 & -2\\ 0 & 1 & -1 ...
...[
\begin{array}
{c}
-1\\ -5\\ 6\\ 7
\end{array} \right]
\end{displaymath}](img1.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccc}
-1 & 2 & 0\\ 2 & -1 & 2\\ 0 & 2 & -1\\ \end{array} \right]
\end{displaymath}](img2.gif)
![\begin{displaymath}
\left[
\begin{array}
{ccccc}
0 & 0 & 0 & 0 & 2\\ 0 & 2 & ...
...2 & 0 & 0 & 0 & 0\\ 0 & 0 & 2 & 0 & 0\\ \end{array} \right]
\end{displaymath}](img3.gif)
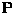 satisfies
satisfies
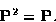
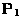 and
and 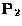 are projection matrices,
then
are projection matrices,
then 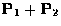 is a projection matrix only if
is a projection matrix only if
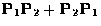 is a zero matrix.
is a zero matrix.
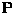 is a projection matrix, then
is a projection matrix, then 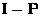 is also a
projection matrix.
is also a
projection matrix.
![$
{\bf M}=
\left[
\begin{array}
{cc}
{\bf A}& {\bf B}\\ {\bf C}& {\bf D}
\end{array} \right],
$](img15.gif) where
where 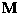 in terms of
the submatrices
in terms of
the submatrices 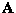 ,
, 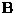 ,
, 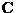 , and
, and 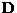 . Specifically, you should start with the identity
. Specifically, you should start with the identity
![$
\left[
\begin{array}
{cc}
{\bf A}& {\bf B}\\ {\bf C}& {\bf D}
\end{array}...
...egin{array}
{cc}
{\bf I}& {\bf 0} \\ {\bf 0} & {\bf I}
\end{array} \right]
$](img20.gif) and expand it into four matrix equations.
Then derive
and expand it into four matrix equations.
Then derive
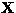 ,
, 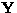 ,
, 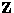 , and
, and 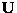 in terms of the
submatrices
in terms of the
submatrices 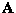 ,
, 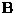 ,
, 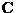 , and
, and 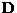 explicitly.
explicitly.
![$
\left[
\begin{array}
{cc}
{\bf X}& {\bf Y}\\ {\bf Z}& {\bf U}
\end{array}...
...gin{array}
{cc}
{\bf I}& {\bf 0} \\ {\bf 0} & {\bf I}
\end{array} \right].
$](img25.gif)
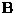 and
and 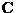 are not necessarily invertible.
So your answers should not include expressions such as
are not necessarily invertible.
So your answers should not include expressions such as
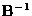 and
and 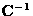 .
.