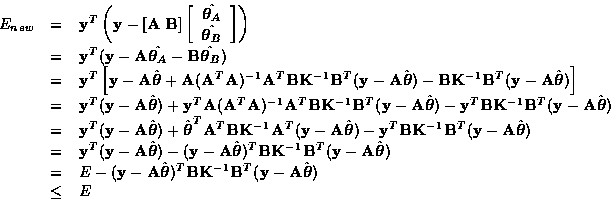Next: About this document ...
Recursive LSE in the Number of Parameters
Before delving into the problem of recrusive LSE in the number of
parameters, we need to know the lemma that expresses the matrix
inverse in a block form:
![\begin{displaymath}
\begin{array}
{rcl}
\left[ \begin{array}
{cc} {\bf A}& {\bf ...
...bf B}^T{\bf A}^{-1} & {\bf K}^{-1}\end{array}\right]\end{array}\end{displaymath}](img1.gif)
where 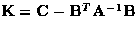 .
.
A set of over-determined linear equations can be expressed as
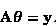
The LSE (least-squares estimator) to the above question is
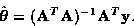
When extra parameters are introduced, the vector 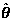 will have more components and the matrix
will have more components and the matrix 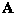 will have additional
columns. We shall derive a recursive LSE formula in the number of
parameters. The new set of over-determined linear equations can be
expressed as
will have additional
columns. We shall derive a recursive LSE formula in the number of
parameters. The new set of over-determined linear equations can be
expressed as
![\begin{displaymath}[{\bf A}\; {\bf B}]
\left[
\begin{array}
{c}
\mbox{\boldmath$...
...a$}_A\\ \mbox{\boldmath$\theta$}_B\end{array}\right] = {\bf y}.\end{displaymath}](img7.gif)
where
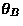 is a vector of newly added parameters and
is a vector of newly added parameters and 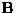 is
corresponding additional columns.
The corresponding LSE can be expressed as
is
corresponding additional columns.
The corresponding LSE can be expressed as
![\begin{displaymath}
\begin{array}
{rcl}
\hat{\mbox{\boldmath$\theta$}}_{new} & =...
...{\mbox{\boldmath$\theta$}})
\end{array} \right],\\ \end{array}\end{displaymath}](img10.gif)
where 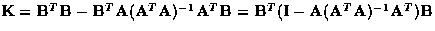 .(Note that if
.(Note that if 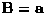 is a column vector, then
is a column vector, then 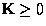 and is
equal to the error measure of fitting
and is
equal to the error measure of fitting 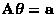 .)
.)
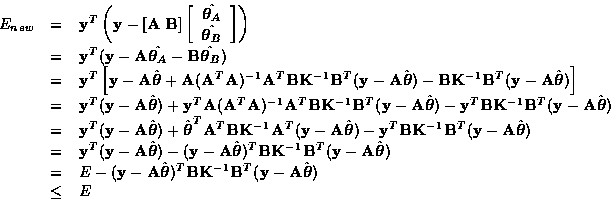
(Note that 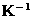 is symmetric.)
is symmetric.)
J.-S. Roger Jang
4/24/1999
![\begin{displaymath}
\begin{array}
{rcl}
\left[ \begin{array}
{cc} {\bf A}& {\bf ...
...bf B}^T{\bf A}^{-1} & {\bf K}^{-1}\end{array}\right]\end{array}\end{displaymath}](img1.gif)
![\begin{displaymath}
\begin{array}
{rcl}
\left[ \begin{array}
{cc} {\bf A}& {\bf ...
...bf B}^T{\bf A}^{-1} & {\bf K}^{-1}\end{array}\right]\end{array}\end{displaymath}](img1.gif)
![]()
![]()
![]()
![\begin{displaymath}
\begin{array}
{rcl}
\hat{\mbox{\boldmath$\theta$}}_{new} & =...
...{\mbox{\boldmath$\theta$}})
\end{array} \right],\\ \end{array}\end{displaymath}](img10.gif)