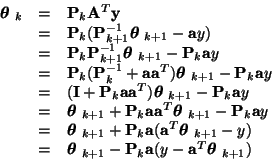Next: About this document ...
Incremental Formula for LSE Error Measures
Let Ek and Ek+1 be the optimal error measures of
the least-squares problems involving k and k+1input-output data pairs, respectively.
In symbol:
(Note that for simplicity, we have left out the
 for the least-squares estimator
for the least-squares estimator
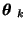 and
and
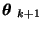 .)
Our mission is to find an incremental formula between
Ek and Ek+1, as follows:
.)
Our mission is to find an incremental formula between
Ek and Ek+1, as follows:
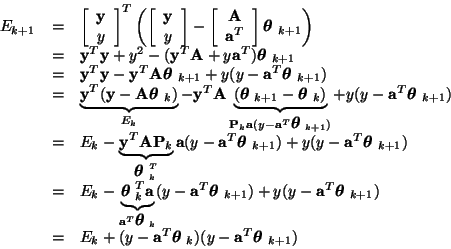 |
(1) |
This concludes our derivation.
Note that in the above derivation, we have used a formula
which can be derived as a side note in the following:
J.-S. Roger Jang
2000-04-06